tags:
- primary-level
- basic-geometry
- geometry
- map-of-content
cssclasses:0-1 Basic geometry index
My pen & paper notes: https://photos.app.goo.gl/DJA4fHQZvwCGjkg5A
Learning checklist:
- Terms: point, line, line segment, ray, colinear, midpoint, planes, planar
- Vertex
- Obtuse, acute, right straight angles
- Notation/naming of angles
- Identify rectangle, rhombus, parallelogram, trapezium (US trapezoid)
- Triangle identify, r.a, scalene, isosceles, equilateral
- Co-ordinate plane: plot points, write ordered pairs including fractional, find distance between points
- Area of parallelogram or triangle
- Area of quadrilaterals with 2 parallel sides
- Volume of tri and rect prisms
- Surface area from a net
- Definitions of pi
- How we give answers as multiples of pi and why
- Circle circumference, cylinder volume, cylinder surface
- Sphere volume, surface
- Cone volume, surface
- Angles: adjacent, complimentary, vertical, supplementary
- Parallels, traversals, angles - be able to identify angles when a traversal crosses parallels
- Triangle inequality theorem, degenerate triangles
- Pythagorean theorem, how to use on isosceles tris, distance formula
- Transformations
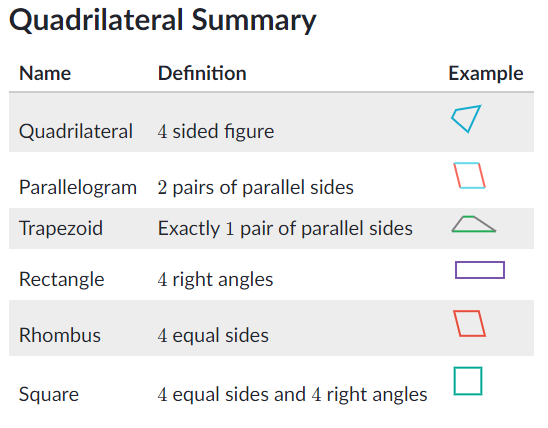
Quadrilaterals review
- Review the following quadrilaterals: parallelogram, trapezoid, rhombus, rectangle, and square. Then, try some practice problems.
Transformations
-
Rigid transforms: rotation, translation, reflection
-
Write the shape and its translation using prime symbol ' [https://en.m.wikipedia.org/wiki/Prime_(symbol)](https://en.m.wikipedia.org/wiki/Prime_(symbol)
-
Three pieces of information are needed to rotate a shape:
- the centre of rotation
- the angle of rotation
- the direction of rotation
-
In reflection A to A' will be perpendicular to line of reflection. To describe a reflection on a grid, the equation of the mirror line is needed. E.g reflect in X= -1
-
Column vectors are used to describe translations.
-
Two pieces of information are needed to enlarge a shape:
- the scale factor
- the centre of enlargement - can be outside shape
-
Congruent shape are same size and shape. One can cover the other via rigid transforms. Can include reflection.
- Triangle congruent tests: SSS SAS ASA RHS
-
Similar shapes need rigid and non rigid transforms to cover each other.
- Similar have corresponding angles the same, and corresponding sides same scale factor.
- Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. Either of these conditions will prove two triangles are similar.
Triangle inequality (lengths)
- A side of a triangle must be:
- Shorter than the sum of the other sides
- Longer than the difference between the other two sides